Optimal control of chaotic turbulent flows

A proper algorithm for non-convex optimization with chaotic dynamics

Optimal flow control problem is to seek an optimal control \(\mathbf{\Theta}^{\ast}\) that minimizes a control objective \(\mathcal{J}\) of a flow state \(\mathbf{q}\). It is often formulated as an equality-constrained optimization,

$$\mathbf{\Theta}^{\ast} = \mathrm{argmin}\;\mathcal{J}[\mathbf{q}]$$ $$\text{such that} \qquad\mathcal{N}[\mathbf{q};\mathbf{\Theta}] = 0,$$

where the equation \(\mathcal{N}\) governs the dynamics of the flow. This optimization problem provides a mathematical framework to tackle many of scientific and engineering goals in fluid dynamics:

  • Passive/active flow control design
  • Grid adaptation and data-assimilated modeling
  • Flow instability analysis.

Gradient-based methods can accelerate finding an optimal solution, using the gradient \(\nabla_{\Theta}\mathcal{J}\) to control. They are particularly effective with high-dimensional optimization spaces. However, this is not true for chaotic turbulent flows. The so-called butterfly effect amplifies the gradient exponentially in time, with extreme sensitivity to initial condition. At the same time, The objective \(\mathcal{J}\) becomes highly non-convex in the optimization space, for which any gradient-based method loses its effectiveness.

An example control objective in the chaotic Lorenz dynamics: its gradient to control amplifies exponentially (left); its non-convex features frustrate searching for an effective local optimum (right).

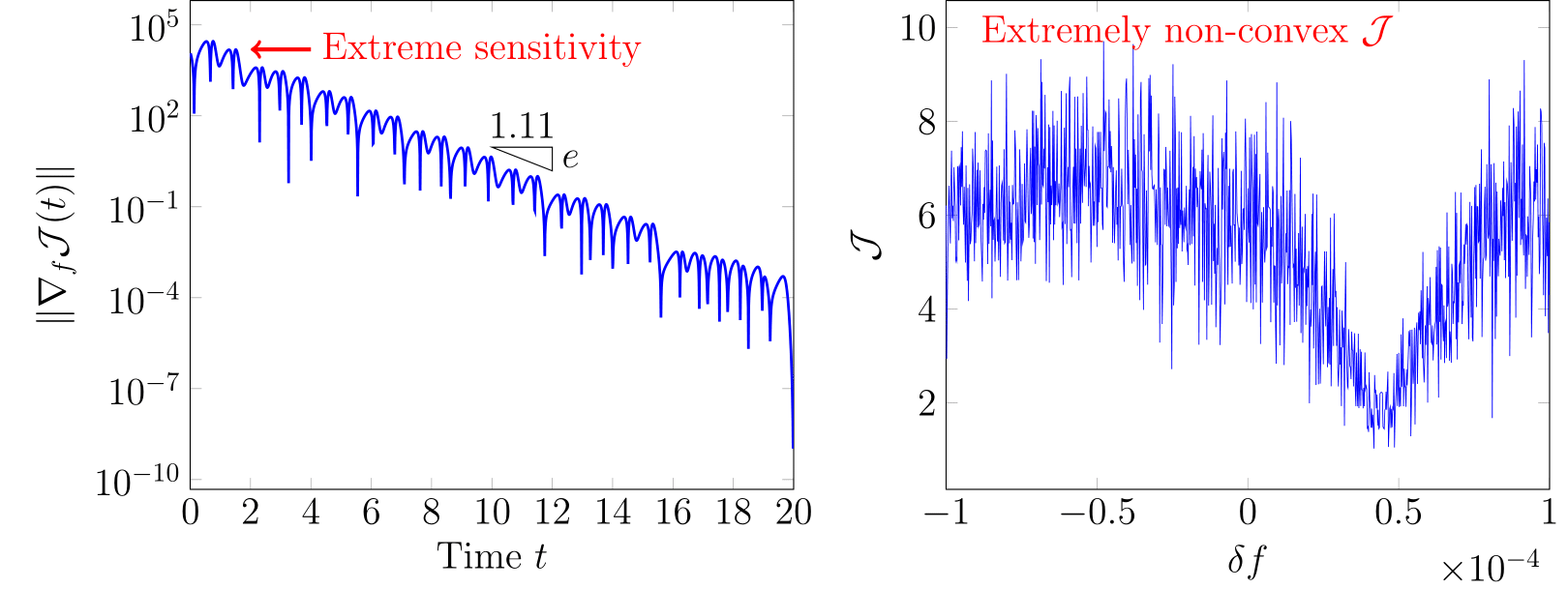
I analyzed the mathematical mechanism of this challenge in the context of horseshoe mapping of chaotic dynamical systems, and proposed a proper optimization framework that can circumvent non-convex optimization. In essence, it temporarily enlarges search scale by introducing intermediate discontinuities in \(\mathbf{q}\), then increasingly penalizes them. As an instance of effective control law, such optimized solution provides a pathway to harness the effective control law and analyze the system. This framework is demonstrated its effectiveness on various flow control problems, including three-dimensional turbulent Kolmogorov flow.

Multi-step optimization for control of the Lorenz dynamics: intermediate discontinuities (red) are temporarily introduced, then increasingly penalized.
Pressure control of turbulent Kolmogorov flow: Q-criterion iso-surfaces colored by pressure perturbation.