Sensitivity analysis in plasma kinetics
Regular sensitivity computing algorithm in chaotic particle dynamics simulations
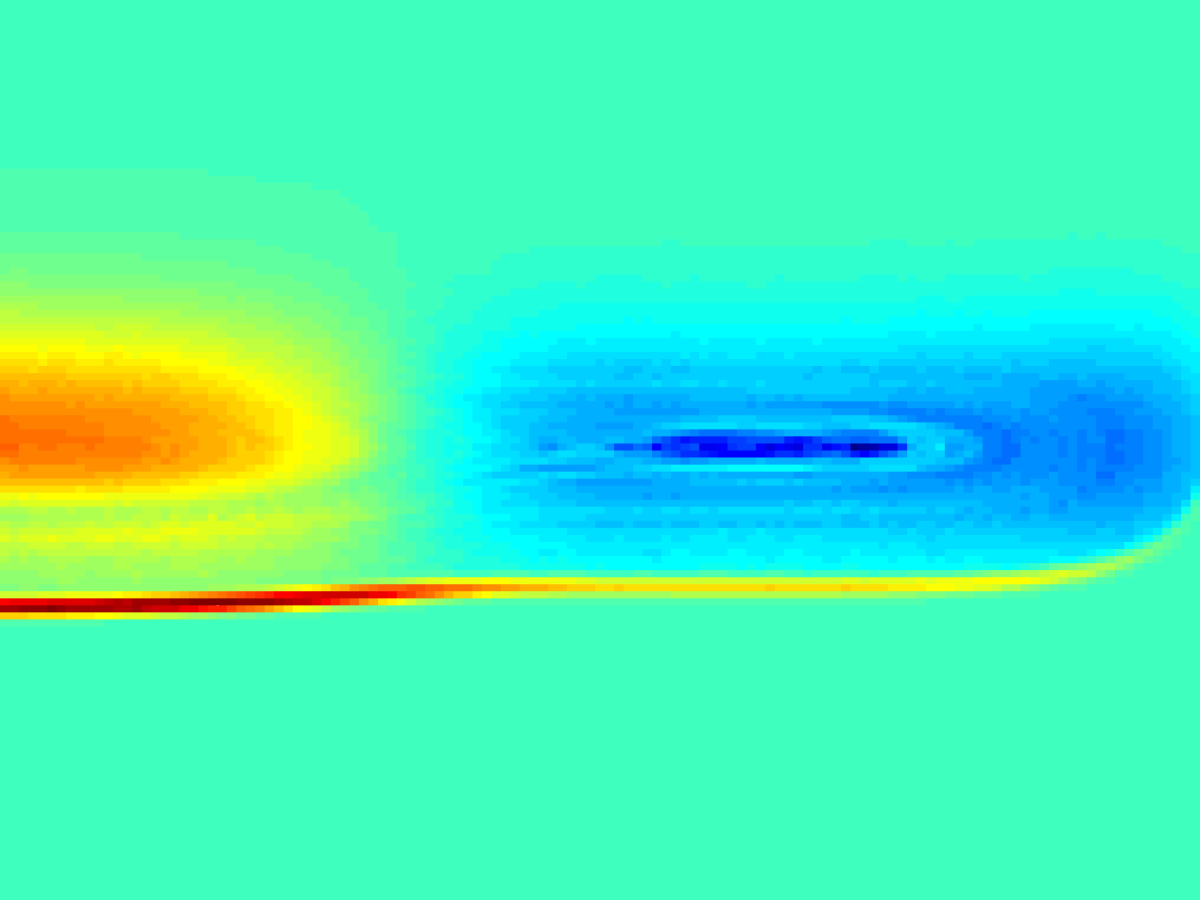
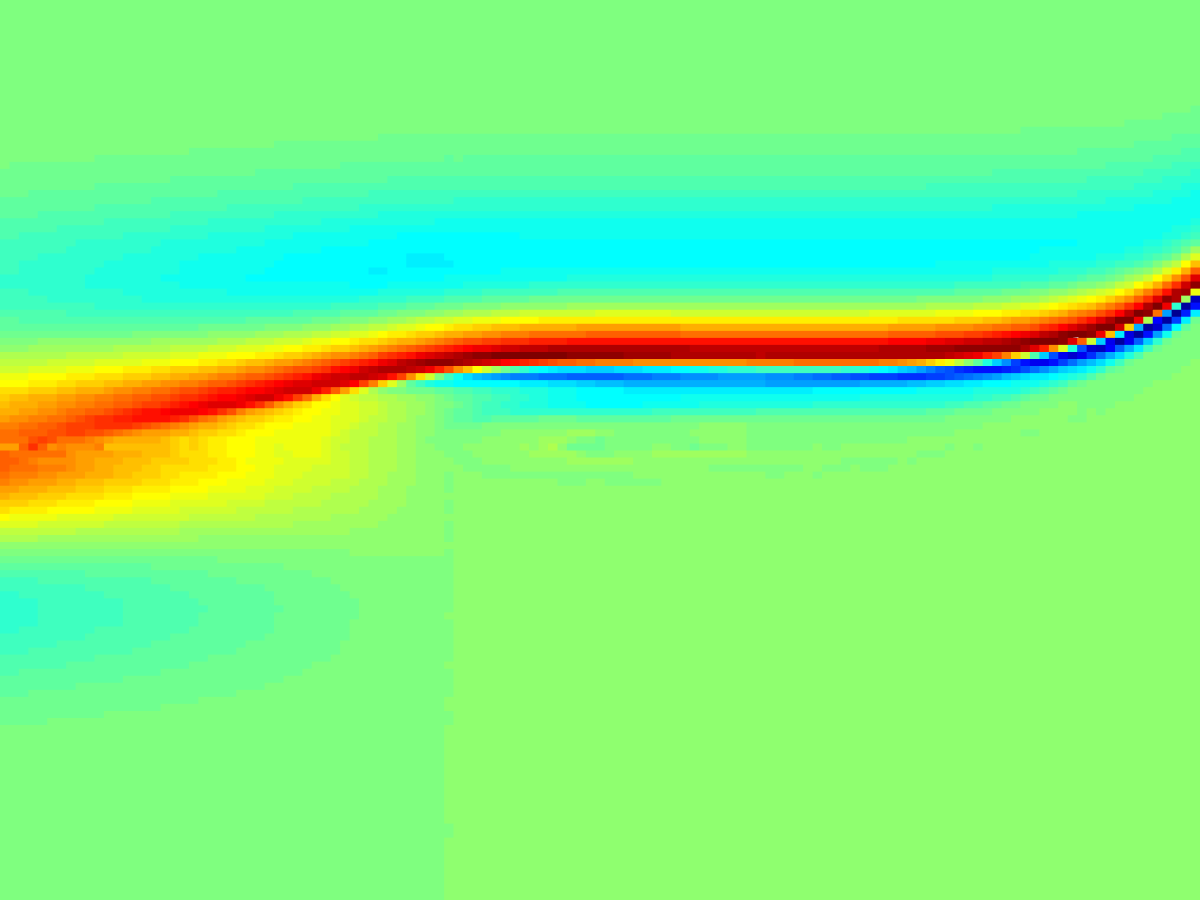
Particle-in-cell (PIC) method is an effective simulation tool for plasma kinetics, where velocity distribution of plasma species deviates from equilibrium and often does not remain stationary. While mesh-based methods suffer from high-dimensional space-velocity phase space, PIC method utilizes coarse-grained Lagrangian particles to represent the plasma distribution with amenable computational costs.
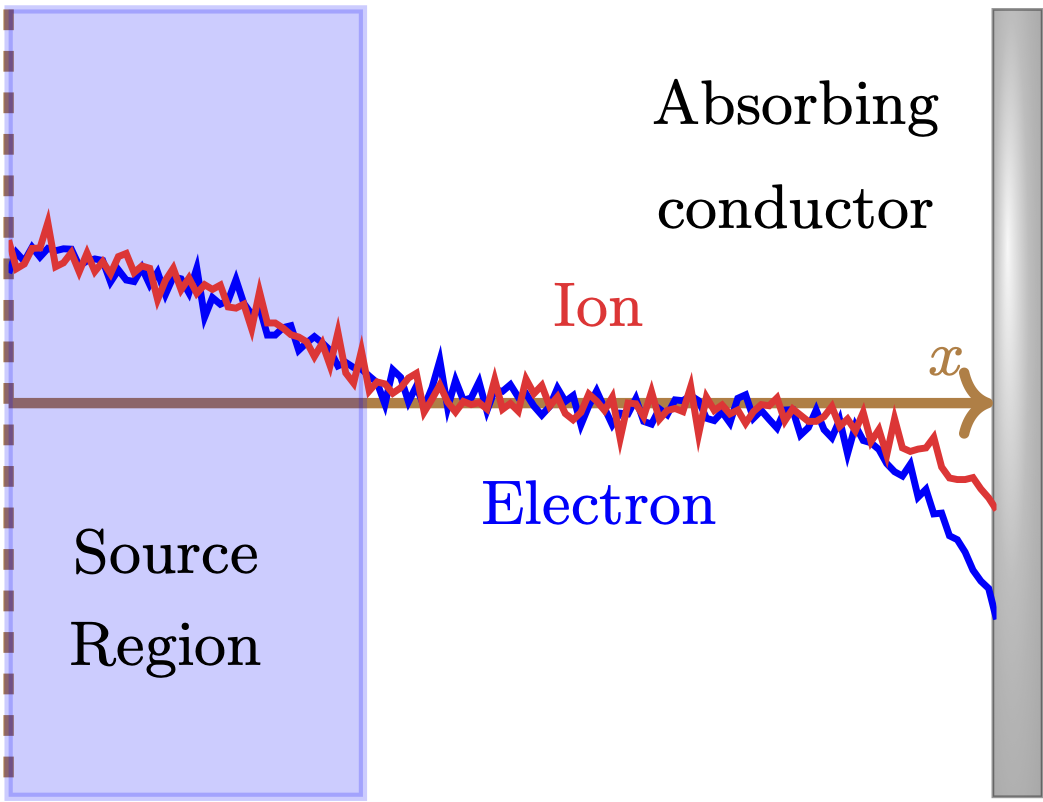
PIC simulation can benefit from sensitivity analysis, which provides a gradient of a quantity-of-interest \(\mathcal{J}\) to parameters-of-interests \(\mathbf{\Theta}\). Such gradient can be used to:
- design optimization
- uncertainty quantification.
Computing the sensitivity in PIC simulations, however, is challenging. Simulation particles mimicks the chaotic \(N\)-body dynamics of actual molecules, which are extremely sensitive to their initial conditions. While there is an ‘useful’ sensitivity of the plasma distribution as a whole, exploding sensitivities of individual particles mask it to be computed exactly.
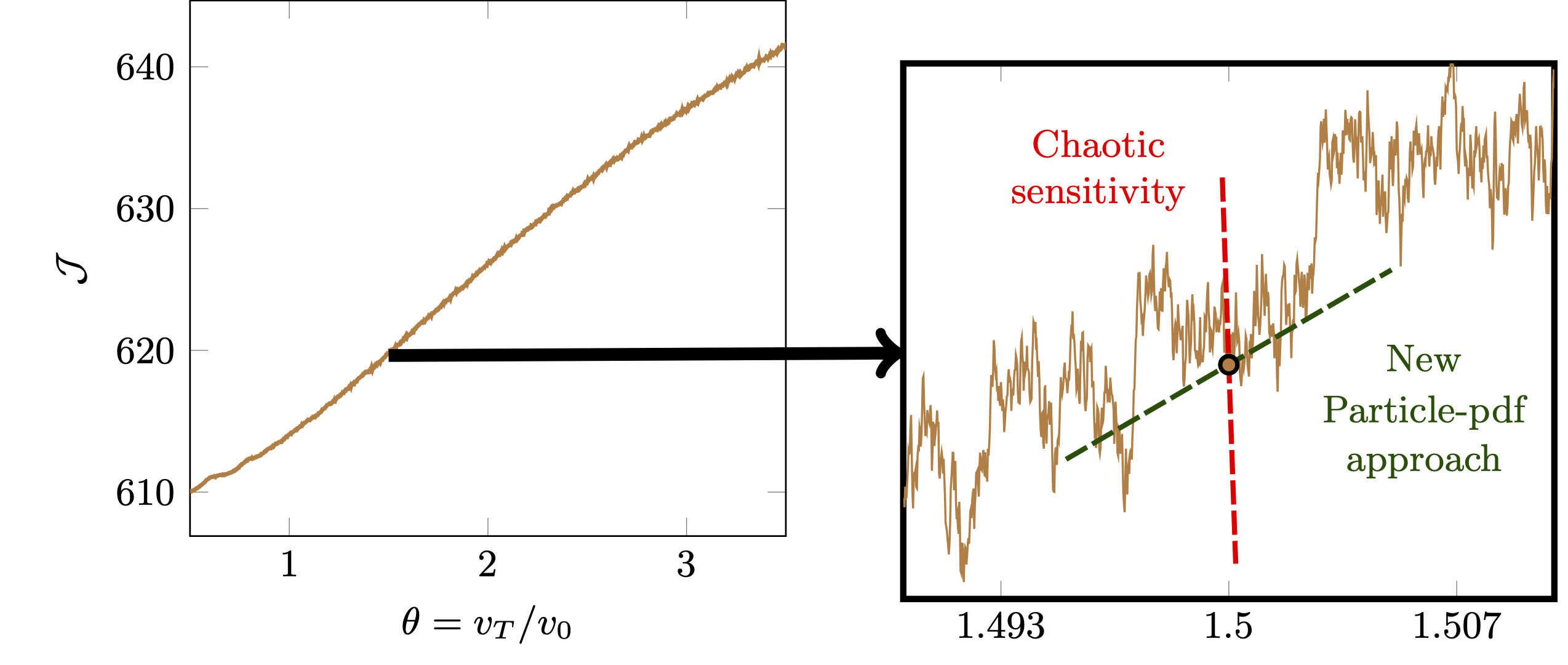
Debye-shielding length scale \(\mathcal{J}\) as a function of electron thermal velocity \(v_T\) (left). Due to chaotic particle dynamics, \(\mathcal{J}(v_T)\) becomes extremely non-smooth (right).
I proposed and developed the particle-pdf approach, where the adjoint particles represent the sensitivity of plasma distribution, not individual plasma particles. The proposed approach avoids chaotic sensitivities of particles and computes the useful sensitivity at a computational cost similar to the original plasma simulation.